مقدمه

در پیش بینی های فروش، مواردی پیش می‌آید که داده‌های فروش گذشته، توزیع نرمال ندارند. به این ترتیب بیشتر پیش‌فرض‌های مربوط به پیش بینی های فروش محقق نشده و نتایج حاصل از آن‌ها ممکن است باعث گمراهی تحلیلگر شود. سوالی که اینجا پیش می‌آید این است که اگر داده‌های فروش گذشته، توزیع نرمال نداشته باشند، چه باید کرد؟

در حقیقت به دنبال روش‌هایی هستیم که بتوان تحلیل‌های آماری را برای توزیع‌های غیر نرمال انجام داد. کاربرد قضیه چبیشف و دیگر روابطی که برمبنای احتمال نوشته می‌شوند می‌تواند به عنوان مبنای تحلیل‌های جایگزین در زمان نرمال نبودن داده‌ها، باشد.

کاربرد نامساوی چبیشف

اگر شرط نرمال بودن داده‌های فروش وجود نداشته باشد، استفاده از این قضیه و کران‌هایش، می‌تواند شاخصی برای نمایش میزان تراکم و یا پراکندگی داده‌ها حول میانگین ارائه دهد. هنگامی که مشخص شود که توزیع داده‌ها نرمال هستند، می توان به راحتی با استفاده از قواعدی که در خصوص توزیع نرمال برقرار است به تحلیل و پیش بینی فروش دوره آتی که مفهوم و قابل درک هست اقدام کرد. در عین حال ممکن است که شرط نرمال بودن برای مجموعه داده برقرار نباشد. در اینصورت نیاز داریم تا از قضایا و روابطی استفاده کنیم تا بتواند در این شرایط پیچیده ما را در پیش بینی های فروش کمک کند.

فرض کنید پس از جمع آوری آمار فروش گذشته شرکت ، می‌خواهید بدانید که آیا آن‌ها معنی‌دار هستند. در اینجا معنی‌دار بودن به این شکل بیان می‌شود که آیا داده‌ها در کران‌های مورد انتظار شما، قرار دارند یا خیر. معمولا در ابتدای کار تحلیل داده‌ها، میانگین و انحراف استاندارد داده‌ها را محاسبه می‌کنیم تا نسبت به آن‌ها شناخت بیشتری پیدا کنیم. در ادامه بررسی می‌کنیم که داده‌های جدید در چه فاصله‌ای از میانگین برحسب انحراف استاندارد قرار می‌گیرند و یا انتظار است چه درصدی از داده‌ها در فاصله‌ای خاص قرار گرفته باشند. اگر قرار است در سطح اطمینان 95٪ تجزیه و تحلیل‌ها را انجام دهیم، انتظار داریم که داده‌ها در فاصله دو انحراف استاندارد از میانگین قرار داشته باشند. یا بعبارتی دیگر داده های ما توزیع نرمال داشته باشند.

اما اگر این شرط برقرار نباشد، یعنی توزیع جامعه آماری، نرمال نباشد، چه اتفاقی خواهد افتاد؟ در اشکال زیر مشاهده می کنید که تمجع داده های فروش می تواند در سمت راست یا چپ باشد و حالت قرینه توزیع نرمال را نداشته باشد.

پس دیگر نمی توانیم مشابه توزیع نرمال بگوییم که داده های ما در فاصله میانگین و یک انحراف استاندارد، حدود 34.1٪ از مشاهدات وجود دارد.

در حقیقت ما به دنبال راه حلی هستیم که به کمک آن بتوان عبارت زیر را بیان کرد: «احتمال آنکه یک داده از مشاهدات جدید در یک فاصله مشخص از میانگین قرار داشته باشد برابر است با …»

خوشبختانه کران‌های نامساوی چبیشف قادر است مشکل را برطرف کند. این نامساوی به افتخار دانشمند روسی «پافنوتی چبیشف» (Pafnuty Chebyshev) نام‌گذاری شده است. او در سال 1853 اثبات این نامساوی را ارائه و منتشر کرد.

از آنجایی که این قضیه بدون فرض نرمال بودن توزیع ایجاد شده است، از آن برای پیدا کردن کران‌ها برای داده‌هایی با هر توزیع احتمالی، می‌توان استفاده کرد. به این ترتیب بدون آگاهی از مکانیزم تولید یا توزیع داده‌ها می‌توان گفت: «من با اطمینان 75٪، می‌دانم که داده‌ها در فاصله 2 انحراف استاندارد از میانگین قرار دارند.»

یا عبارتی مانند زیر را برای فاصله سه انحراف معیار بیان کرد: «با اطمینان 89٪، داده‌های در فاصله سه انحراف استاندارد از میانگین قرار دارند.»

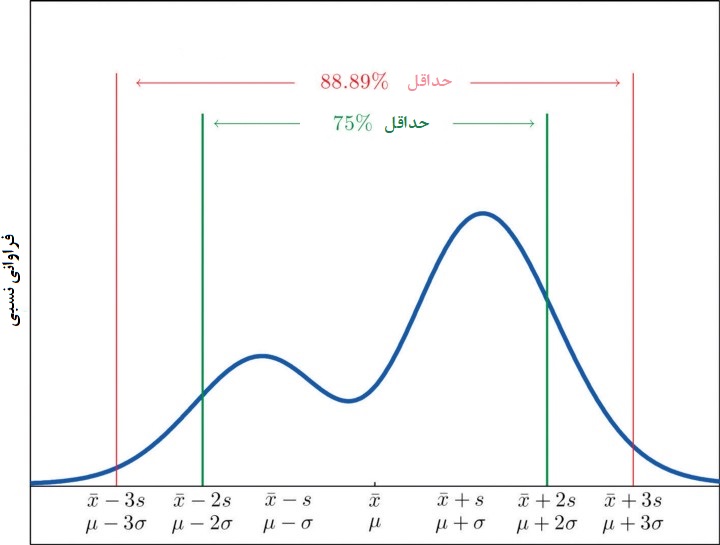
همانطور که دیده می‌شود، اصل محاسبات برای داده‌ها تغییری نکرده است و همچنان میانگین و انحراف استاندارد را برای داده‌ها محاسبه می‌کنیم. ولی برای تعیین احتمالات یا درصدی از داده‌ها که در یک محدوده قرار دارند، باید از نامساوی چبیشف استفاده شود. بنابراین مراحل کار به صورت زیر خواهد بود:

• جمع‌آوری داده‌های نمونه‌ای از یک جامعه آماری با توزیع نامشخص (غیر نرمال)
• محاسبه میانگین و انحراف استاندارد براساس نمونه
• محاسبه کران‌های چبیشف