مقدمه :

روش مورد استفاده برای پیش بینی با استفاده از داده های فروش(حداقل دو داده)، را مدیون فردی به نام ویلیام سیلی گاست(William Sealy Gosset)، یک شیمی دان و آماردان، در شرکت آبجوسازی گینس در دوبلین هستیم. در اوایل قرن بیستم گاست با یک مساله اندازه گیری روبرو شد. او باید راهی را پیدا می کرد که کدام نوع جو بهترین بازدهی را در آبجو سازی دارد. 

پیش از آن، روشی که امتیاز z یا آماره نرمال نامیده می شد( مطلب "توزیع نرمال و کاربرد آن در تحلیل داده ها" را مطالعه کنید) برای برآورد فاصله اطمینان براساس نمونه های تصادفی درست شده بود( البته به شرطی که اندازه نمونه دست کم سی مورد باشد) . این روش توزیع هایی را به شکل توزیع نرمال تولید می کند. متاسفانه، گاست چنین نمونه بزرگی از آبجو برای هر نوع جو در اختیار نداشت. ولی به جای اینکه فکر کند نمی تواند اندازه گیری را انجام دهدف نوع جدید از توزیع را برای نمونه های با اندازه بسیار کوچک ابداع کرد.

این روش، آماره t یا آماره t استیودنت(student)، نامیده می شود. شکل آن مشابه توزیع نرمال است که پیشتر درباره آن صحبت کرده بودیم. برای نمونه ای با اندازه بیش از سی، شکل توزیع t کمابیش مشابه توزیع نرمال است. ولی برای نمونه های بسیار کوچک، شکل توزیع، صاف تر ، عریض تر و دنباله ها ضخیم تر هستند. فاصله اطمینان 90 درصد محاسبه شده با روش آماره t، عدم قطعیتش بسیار بیشتر از همان فاصله اطمینان در توزیع نرمال است.

روش محاسبه :

فرض کنید فروش فروردین ماه 5 سال گذشته یک شرکت تولید کننده لامپ های لیزری به ترتیب اعداد 300، 600، 450، 800 و 950 باشد. این شرکت می خواهد برای فروردین سال جاری براساس داده های گذشته دست به پیش بینی بزند.

1) با استفاده از اکسل، ابتدا میانگین نمونه ها را با استفاده از فرمول average محاسبه کنید. میانگین فروش 5 ساله گذشته 620 می شود.

2) انحراف معیار داده های فروش را بدست آورید. برای انحراف معیار، می توانید از فرمول stdev.s استفاده کنید. حاصل این محاسبه عدد 116.8 می شود.

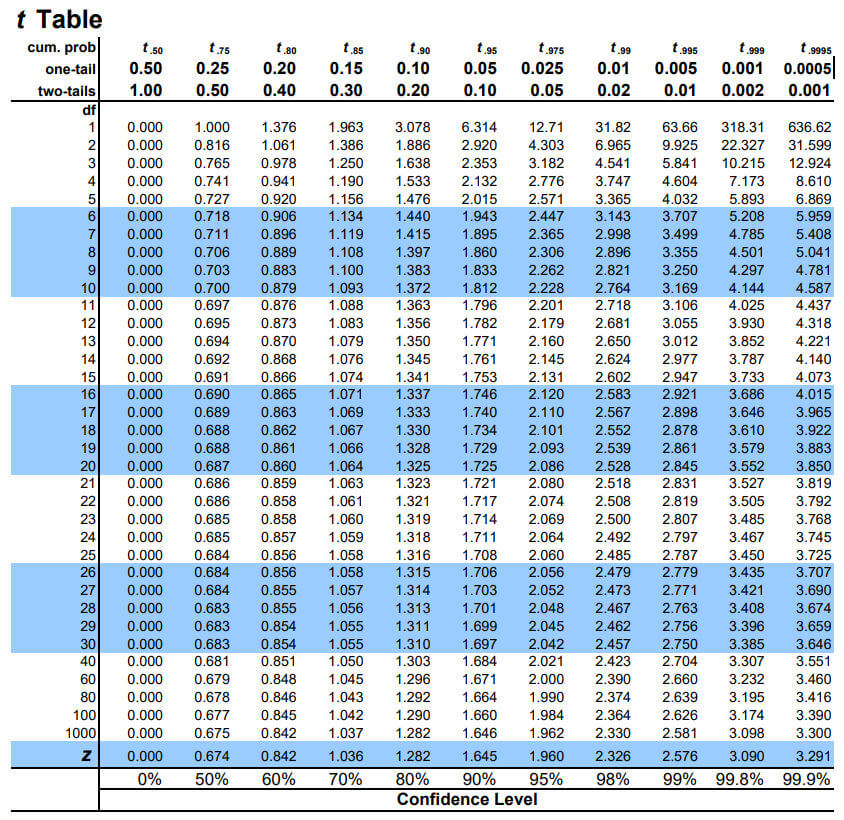
3) با استفاده از جدول t استیودنت، تعداد نمونه ها را پیدا کنید( در اینجا 5 نمونه داریم)، سپس در فاصله اطمینان که مدنظر شماست، امتیاز t را یادداشت کنید. با فاصله اطمینان 95 درصد، امتیاز t، عدد 2.015 می باشد.

4) آماره t را در عددی که در گام دوم بدست آورده بودیم (انحراف معیار)، ضرب کنید. عدد بدست آمده 235.4 خواهد شد. این عدد خطای نمونه را برحسب واحد فروش ما نشان می دهد.

5) خطای بدست آمده را با میانگین جمع بزنید تا کران بالای فاصله اطمینان 95 درصد بدست آید. سپس از میانگین کم کنید تا کران پایین این فاصله بدست آید. به کران بالا، خوشبینانه یا حد بالا و به کران پایین بدبینانه یا حد پایین نیز گفته می شود. برای مثال ما کران بالا و پایین فروش فروردین امسال بترتیب اعداد، 855 و 385 خواهد بود. می توان از روش میانگین وزنی و یا میانگین ساده برای برآورد فروش فروردین نیز استفاده نمود.