مقدمه :

توماس بیز( Thomas Bayes) ( 1702 - 1761) ریاضیدان انگلیسی است که به دلیل فرمول‌بندی حالت خاصی از قضیه بیز، معروف گشته‌است. 

قضیه بیز از آن جهت مفید است که می توان از طریق آن، احتمال پیشامدی را با مشروط کردن آن پیشامد نسبت به وقوع یا عدم وقوع پیشامدی دیگر محاسبه کرد. این قضیه به لحاظ منطقی راهی را پیش پای ما می گذارد تا در آن بتوانیم از تناقض بین آنچه گمان می کنیم درست است، با اطلاعاتی که بعدا و طی مسیر به دست ما می رسد جلوگیری کنیم.

قضیه بیز ما را وادار می کند درباره تمام پیش بینی ها، اتفاقات و مشاهداتمان سوالات بسیار جدی و کاوشگرانه ای مطرح کنیم. برای مثال به جای اینکه بپرسیم:"چقدر احتمال دارد یک دونده المپیک از مواد نیروزا استفاده کرده باشد؟"، باید بپرسیم:" با اینکه می دانیم نتیجه آزمایش این دونده مثبت درآمده و با علم به اینکه جواب آزمایش ها در شرایط مختلف باهم فرق می کند، چقدر احتمال دارد این دونده مواد نیروزا استفاده کرده باشد؟".

قضیه بیز راهی جلوی پای ما می گذارد تا محاسبه کنیم انسان اطلاعات جدیدی را که به دستش می رسد چطور ارزیابی و بازنگری می کند. این قضیه فرض را بر این می گذارد که هرکس با استفاده از اطلاعات به دست آمده جدید، باورهای خود را دوباره به آزمون می گذارد تا متوجه شود آیا اطلاعات جدید بدست آمده با باورها و نتیجه گیری های قبلی او سازگاری دارد یا در تضاد است.

بطور کلی این قضیه نشان می دهد باورهای ما در تقابل با اطلاعات جدید که بدست آمده چطور تغییر می کند و بروز می شود. به این ترتیب مشاهده می شود باورها و اندیشه های ما انعطاف پذیرتر از آنند که همچون عقاید کج و معوج و متعصبانه در مغز انسان لانه کنند.

قضیه بیز در پیش بینی ها

در احتمالات شرطی وقتی در رابطه با اتفاقی اطلاعات جدیدی بدست می آید، تجدید نظر کردن در مورد احتمال وقوع آن حادثه، مرحله ی مهمی در تحلیل احتمالات است.

در اغلب موارد، تحلیل ها براساس محاسبه ای از احتمال اولیه یا پیشین وقوع یک پیشامد آغاز می شود و سپس وقتی اطلاعات جدیدی در رابطه با آن پیشامد به دست می آید، در احتمال پیشین تجدید نظر شده و احتمال جدیدی برای آن محاسبه می شود. به این احتمال جدید بازنگری شده اصلاحا احتمال پسین می گویند.

قضیه بیز فرمولی را اریه می کند تا بتوانیم احتمال جدید را محاسبه کنیم. فرآیند کار را در شکل زیر ملاحظه می کنید:

فرمول رابطه ی بیز برای محاسبه احتمال پسین بصورت زیر است :

برای روشن شدن موضوع، به مثال زیر توجه کنید:

دریک کارخانه مواد شیمیایی، پیش بینی شده است، احتمال بروز هریک از حوادثی که می تواند به آتش سوزی منجر شود، می تواند شامل موارد زیر باشد:

• سهل انگاری پرسنل : 40 درصد
• نقص فنی : 50 درصد
• خرابکاری : 10 درصد

در عین حال، پیش بینی های کارشناسان نشان می دهد، چنانچه هریک از حوادث بالا اتفاق بیفتد، احتمال آنکه آن اتفاق باعث آتش سوزی شود، عبارتست از:

• سهل انگاری پرسنل : 30 درصد
• نقص فنی : 20 درصد
• خرابکاری : 90 درصد

حال اگر مطلع شویم که هم اینک آتش سوزی در کارخانه رخ داده است، پیش بینی شما درباره احتمال خرابکاری در کارخانه چقدر است؟

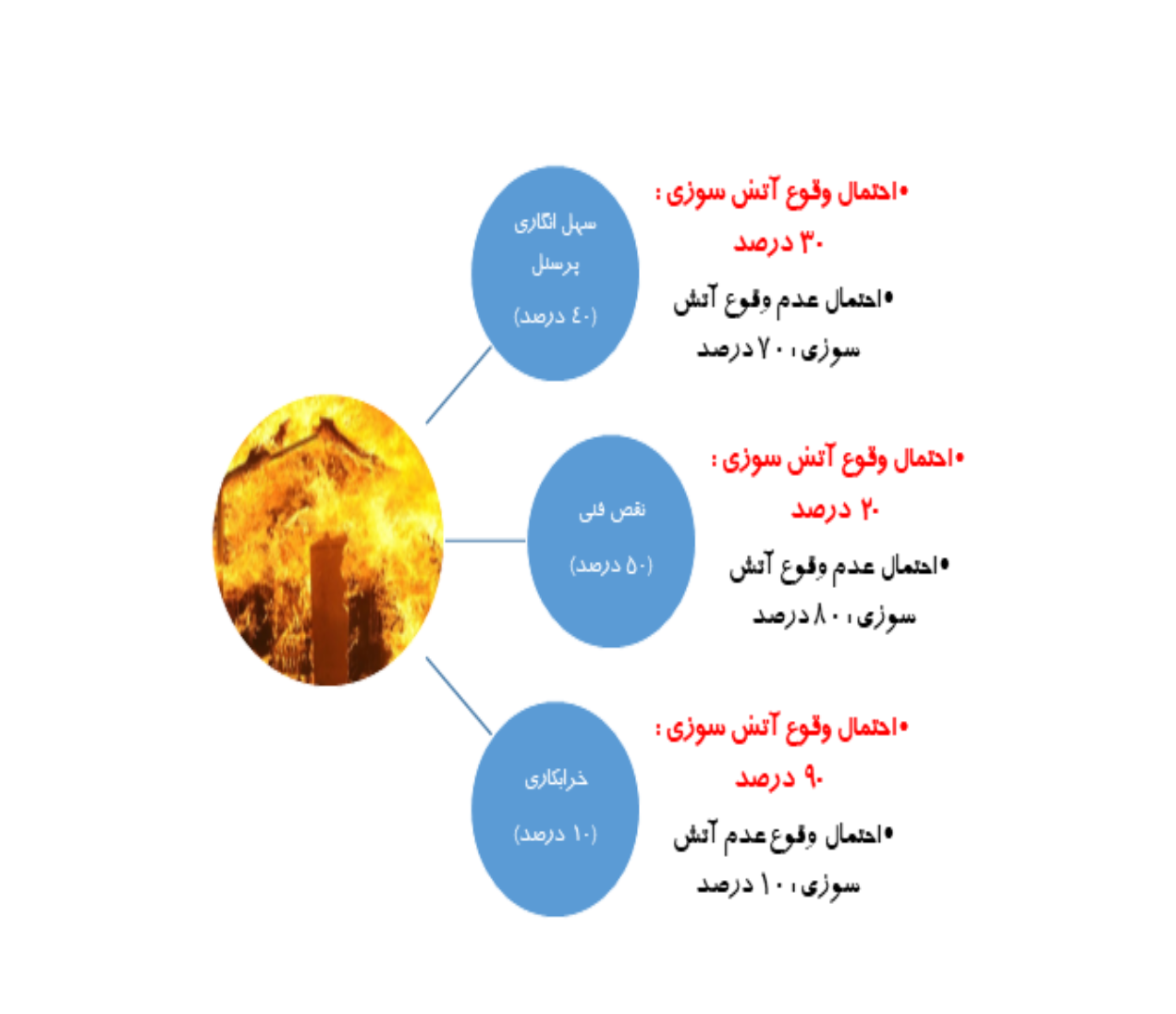
با توجه به اطلاعات مساله، برای اطمینان از صحت پیش بینی های قبلی خودمان، از طریق قضیه بیز خواهیم داشت:

توجه کنید که اطلاع از بروز آتش سوزی، پیش بینی گذشته ما مبنی بر خرابکاری در کارخانه را در این موقعیت از 10 درصد به 29 درصد افزایش می دهد.

در رابطه ی بالا می بینید که همواره آنچه در صورت کسر رابطه ی بیز قرار می گیرد، حاصل ضرب احتمال های مربوط به شاخه مورد نظر است و جمع ضرب احتمال های کلیه شاخه ها نیز در مخرج کسر قرار می گیرد.